前回の最後に

$a_{1}=1$
$a_{n+1}=2a_{n}+3^{n}+n$ ・・・①

をどうやって解くか？みたいな問題あったけど。

実はこれも「掛け続ける」パターン、つまり特性方程式を組み合わせれば解けるっていうオモロい問題。

前回もいったように、
$d_{n+1}=2d_{n}+3^{n}+n$
を満たす数列 $\left\{ d_{n}\right\}$ がひとつ見つかってしまえば、①が解けてしまう。

・・・でも難しい。。ということでとりあえず、
$b_{n+1}=2b_{n}+3^{n}$ ・・・②
を満たす数列 $\left\{ b_{n}\right\}$ と、

$c_{n+1}=2c_{n}+n$ ・・・③
を満たす数列 $\left\{ c_{n}\right\}$

を見つけることにしよう。

というか、とりあえず見つけたことにしよう！

そしたら② $+$ ③より

$b_{n+1}+c_{n+1}=2\left( b_{n}+c_{n}\right) +3^{n}+n$
となる。
ここで
$d_{n}=\left( b_{n}+c_{n}\right)$ と置いてみれば、

$d_{n+1}=2d_{n}+3^{n}+n$ ・・・④

となる！！！すごい！！

あ、あたりまえかな？？

つまり、 $\left\{ b_{n}\right\}$ と $\left\{ c_{n}\right\}$ が見つかった時点で、この漸化式は解けてしまうんだ。

じゃあ実際に $\left\{ b_{n}\right\}$ と $\left\{ c_{n}\right\}$ を求めよう！ってなるけど

$\left\{ c_{n}\right\}$ は前回求めたね。
$c_{n}=-n-1$
だね。

つぎに $\left\{ b_{n}\right\}$ だけど、これは

$b_{n}=a\cdot 3^{n}$ として予想してみよう。これを②に代入すると、

$a\cdot 3^{n+1}=2a\cdot 3^{n}+3^{n}$
$\therefore a=1$

となるから、 $b_{n}=3^{n}$ といえる。

以上より、

$d_{n}=3^{n}-n-1$ だから、① $-$ ④より、

$a_{n+1}-d_{n+1}=2\left( a_{n}-d_{n}\right)$
$a_{n}-d_{n}=2^{n-1}\left( a_{1}-d_{1}\right) =0$
$\therefore a_{n}=d_{n}=3^{n}-n-1$

となる。以上より数列 $\left\{ a_{n}\right\}$ の一般項は

$3^{n}-n-1$

である。

という感じ。これは便利だしたのしいねえ。

2016-09-16

覚えた方がいい「同値変形」

これは覚えたほうがいい。暗記ではないけど。
まず覚えなくていい「必要・十分条件」 - 算数は得意なのに数学が苦手なひとのためのブログの最後に書いたやつを例にとります。

まず最初にいっておくと、方程式とか不等式を「二乗」するときはめちゃめちゃ気を付けないといけない！

じゃあまず、教科書通りに解きます。

$\sqrt {x^{2}-4}=x+1$ ・・・①
両辺を二乗すると、
$x^{2}-4=x^{2}+2x+1$ となるので、これを解くと、 $x=-\dfrac {5}{2}$ となる。
これを①に代入すると成り立たないので、求める解は、
ナシ。

という感じ。

ということで次は、同値変形で解く解き方！

$\sqrt {x^{2}-4}=x+1$
$\Leftrightarrow x^{2}-4=x^{2}+2x+1$ かつ $x+1\geq 0$
$\Leftrightarrow x=-\dfrac {5}{2}$ かつ $x\geq -1$
$\Leftrightarrow$ 解なし

といった感じ。

どういうことかというと、二乗するってことは
$2=-2$
といった間違った式も二乗して
$4=4$
となって合っている式になってしまう。つまりちょっとアヤシイことをしてるわけ。

つまり、二乗する前から符号が分かってるときは、その条件を書かないと同値じゃなくなるんだ。

$\sqrt {x^{2}-4}$ は $0$ 以上だから、二乗しても同値にするためには、 $x+1$ も $0$ 以上だっていう条件が必要。

よって、 $\sqrt {x^{2}-4}=x+1$
$\Leftrightarrow x^{2}-4=x^{2}+2x+1$ かつ $x+1\geq 0$
という変形になる！

この同値変形ができるかどうか、っていうのが「高校数学を勉強したぞ！」って自信持って言えることの必要条件だと思うんだけど、
国立以外の大学の数学の問題って大抵マーク式だったりするからあんまし意味ないなあ、と思ってしまう。

個人的には高校数学って、感覚で思った「なんとなく」を論理で正しく伝える選手権だと思ってるから。

っていってるひとがいた。ってことにしとこう笑

2016-09-16

覚えなくていい「必要・十分条件」

中学受験の算数で身につくチカラって、図形把握力とか図をかく力とか発想力とかだと思う。

それとは違って、大学受験の数学でつくチカラは、発想力とかよりは「論理的思考力」だと思う。

算数では発想そのものを教わったりするけど、数学は論理が大事で、「なんとなくの感覚」すらがんばって言語化して論理で説明することが求められる。

おそらく「オトナ」として当たり前に必要なめちゃめちゃ大事な力だけど、割と苦手なひとがいて避けて通りがち

ということで、論理とかの分野の代表の「必要・十分条件」だけど

これって一度納得してしまえば、そんな難しいもんじゃない。

母校の男子校、栄光を例にとって考えてみよう。（もっと有名な開成とかにしようとおもったけどなんか使うのがおこがましかった笑）

まずこの文章はただしいだろうか？

「栄光生ならば、男である」

当たり前だけど、これは正しい。男子校な時点で、悲しいことに生徒は全員男。

こんな文章のように、「真」か「偽」で答えられる文章のことを「命題」っていう。知ってるだろうけどいちおう。
この文章は正しいから「真」だね。

ここまではつまづく人あんましいないと思う。

ただ、

「じゃあ、栄光生であることは男であるための何条件か？」

みたいな聞かれ方をしたらすこし困るひとが多いと思う。

日本語で説明すれば、

「栄光生であるためには、少なくとも男であることが必要」だから
「男であることは栄光生であるための必要条件」
てことで、

「男であることを証明するためには、栄光生だよ！っていえば十分」だから
「男であるためには、栄光生であれば十分」つまり、
「栄光生であることは男であるための十分条件」

ということなんだけど、毎回こんなかんじで考えるのは大変そう..

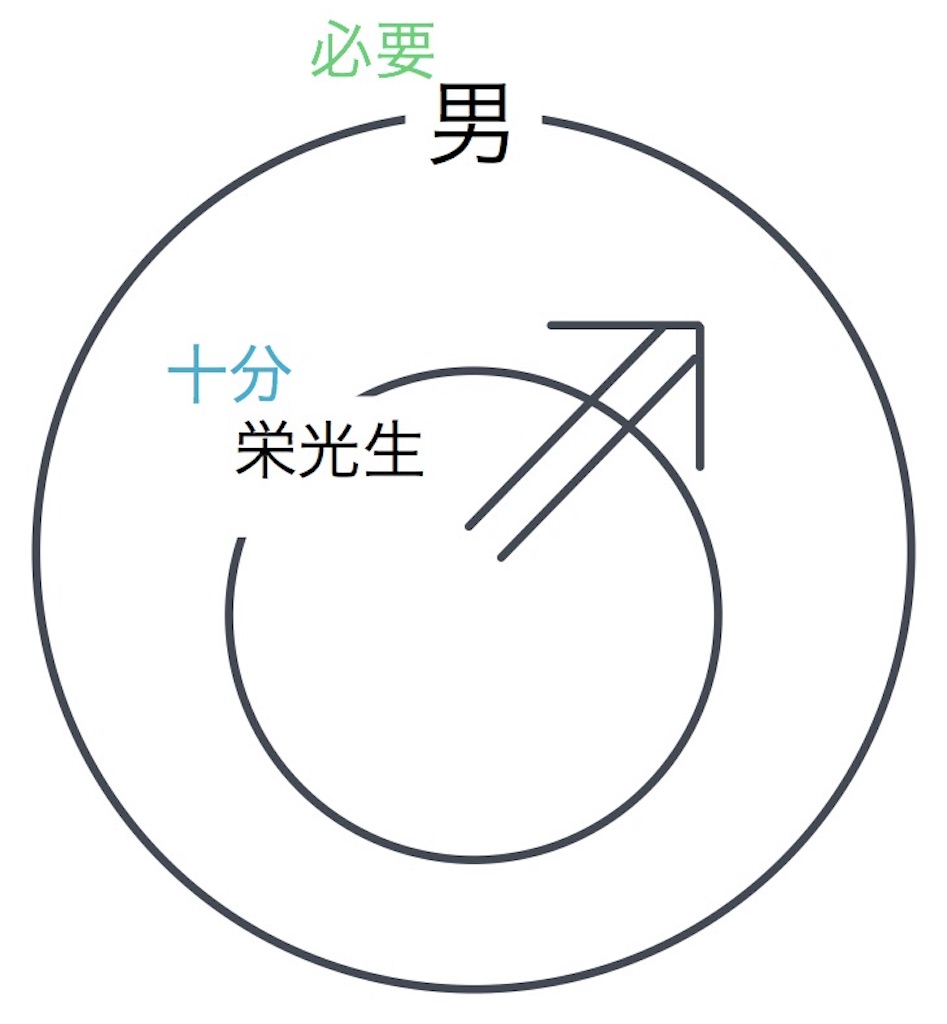
てことで図を書いてみた。

さっきの命題みたいに、十分条件か必要条件かみたいな質問されたらこの図をかけばいい。

この図はなにをいってるかというと、それぞれの個数などを比較したときに、デカいほうが男、小さいほうが栄光生。

つまり、「小さい方」⇒「デカい方」っていえる。

なんで多い少ないじゃなくて、デカい小さいって言い方をしたかというと、

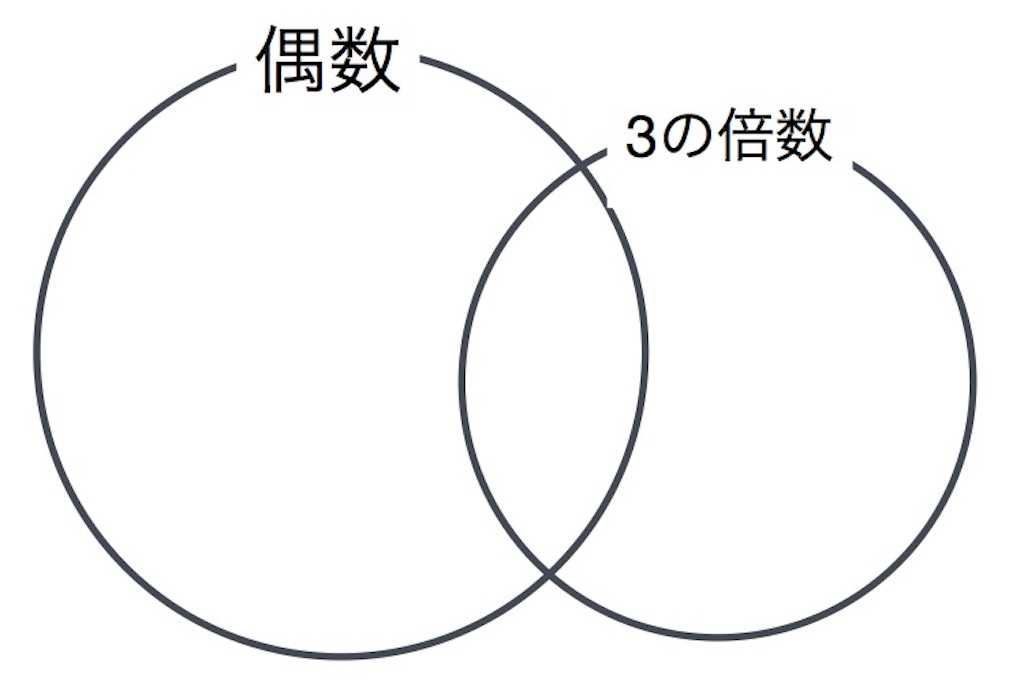
こんなときは偶数の方が多くても、

「3の倍数ならば偶数である」なんていえないからだね。小さい方が、大きい方に完全に包括されてないとダメ。

つまり、必要・十分系の問題はまずベン図を書いてみればいい。

それで包括関係がなかったら、「必要条件でも十分条件でもない」って答えればいいし、全く同じ円になったら「必要十分条件である」でいい。

包括関係だったら、またこのベン図を思い出して比較すればいい

主語がデカい方だったら必要条件。
主語が小さい方だったら十分条件。

たとえば。

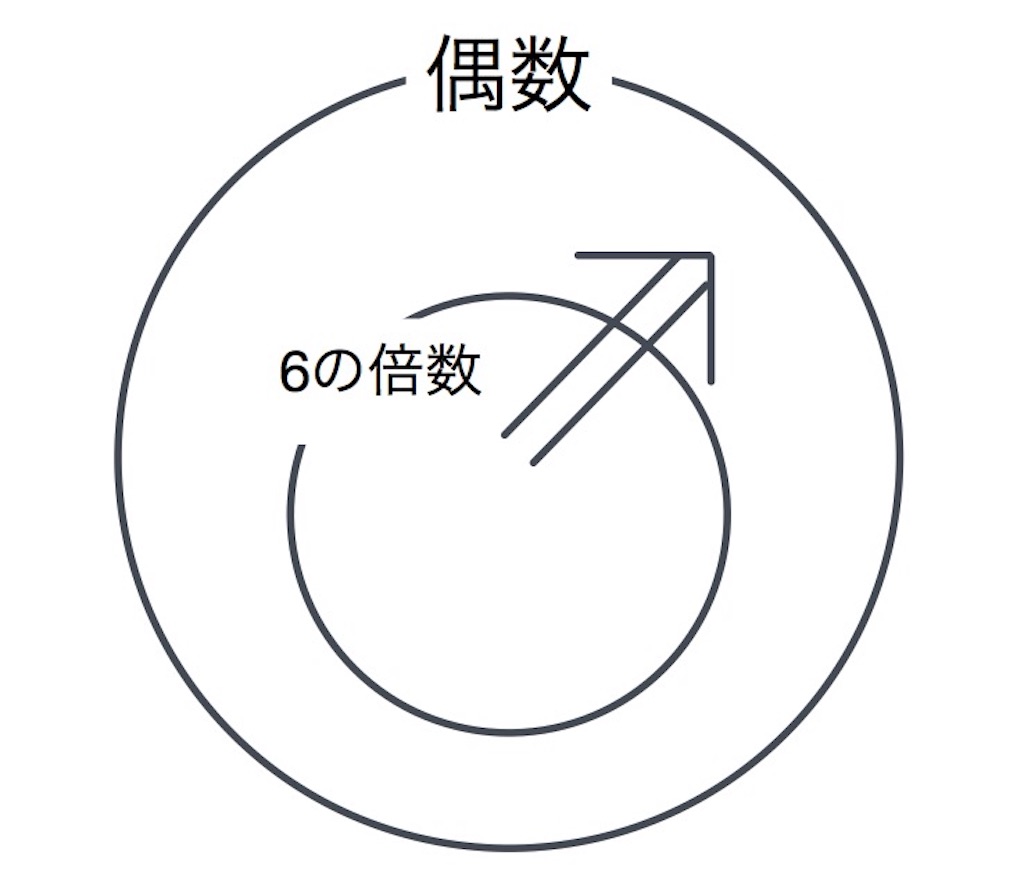
「6の倍数であることは、偶数であるための何条件か？」

と聞かれたら、まずベン図をかいて

6の倍数は「栄光生」とわかるから、答えは「十分条件」

じゃあ、
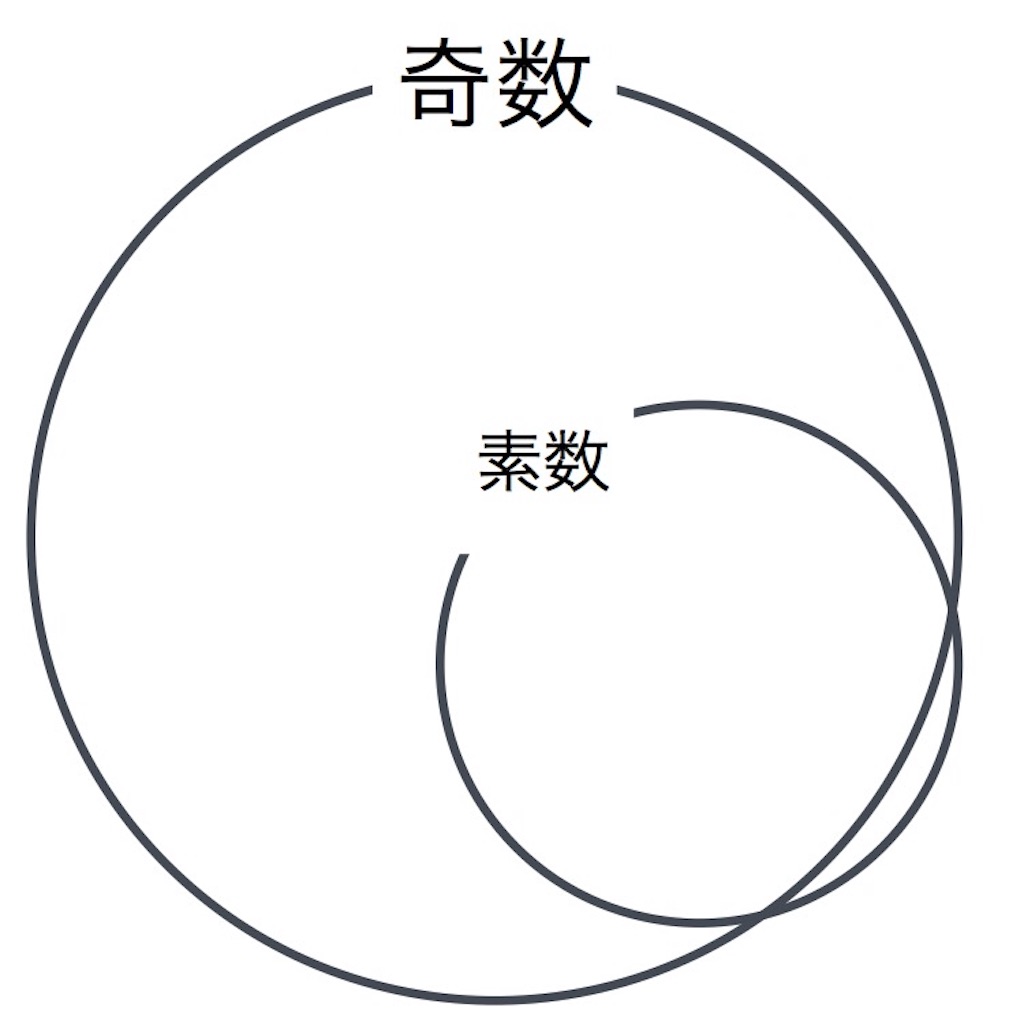
「奇数は素数であるための何条件か？」

これもベン図を書いてみると

必要条件かな？っておもったひともいるかもしれない。

でも素数には奇数じゃない $2$ も含まれるから、包括関係じゃなくなる。ということで、「必要条件でも十分条件でもない」

てことでめちゃ簡単になる。

ちなみに必要・十分条件がわかってると、
$\sqrt {x^{2}-4}=x+1$ の解が、
$x^{2}-4=x^{2}+2x+1$ だから
$x=-\dfrac {5}{2}$ だーっ！
ってやったらアウト！
元の式 $\sqrt {x^{2}-4}=x+1$ に代入して確かめなきゃいけないかってことがわかる。

というかそもそも同値変形をしていけば最後に確認なんてめんどくさいことしなくても済む・・・

ということを次書きます！

2016-09-15

覚えなくていい「数列の一般項」２

http://mynkit.hatenadiary.jp/entry/2016/09/13/234402のつづき

特性方程式ってものは「掛け続けるカタチ」にするためのテクニックだってことは前回いってたとこ。

じゃあ本当に数列 $\left\{ c_{n}\right\}$ なんか見付かるのかよ！

ということで難しそうな例を...

$a_{1}=1$
$a_{n+1}=2a_{n}+n$ ・・・①

の漸化式で表される数列 $\left\{ a_{n}\right\}$ の一般項を求めたい。

ということで、まず
$c_{n+1}=2c_{n}+n$ ・・・②
となる $c_{n}$ をみつけよう。

まず $c_{n}=c$ （定数）と考えると $n$ が残るから無理がありそうだ..

じゃあ $n$ を消したいから $c_{n}=an+b$ みたいな「 $n$ の一次関数的」な感じしてみたらどうだろう？

すると
$c_{n+1}=2c_{n}+n$
$\Leftrightarrow an+a+b=2an+2b+n$
$\Leftrightarrow \left( a+1\right)n-a+b=0$

これが全ての自然数 $n$ について成り立つようにすればいいから、

$a=-1,b=-1$

ならオッケー！ということで、

$c_{n}=-n-1$

がみつかった！ためしに②に代入してみよう。

たしかになりたっている...

ということで、① $-$ ②をすれば

$a_{n+1}-c_{n+1}=2\left( a_{n}-c_{n}\right)$
$\therefore \left( a_{n}-c_{n}\right)=2 ^{n-1}\left( a_{1}-c_{1}\right)$
$\therefore a_{n}=3\cdot2^{n-1}-n-1$

というかんじ。

トクセイホウテイシキってコトバをただ知ってるだけじゃ解けなくても、きちんと理解してればできるんだなあ。

次は、 $a_{n+1}=2a_{n}+3^{n}+n$ みたいなときにどうすればいいかって話しますね。

2016-09-15

覚えなくていい「等比数列の和」

等差数列のときと似たような導入でかきます。覚えなくていい「等差数列の和」 - 算数は得意なのに数学が苦手なひとのためのブログ

まず、等比数列の公式として、
$\left( \sum ^{n}_{k=1}a^{k}\right) =\dfrac {a^{n+1}-a}{a-1}$
こんな感じで教わってるかな？
それとも
$\left( \sum ^{n}_{k=0}a^{k}\right) =\dfrac {a^{n+1}-1}{a-1}$
みたいな感じ？

こんな感じで覚えてると、

$\left( \sum ^{2n}_{k=12}3^{k}\right)$ は？

みたいに聞かれたとき困ります。

ということで

どうせ覚えるなら、「等比数列の和」はこう覚えよう！

「 $\dfrac {最後の次の項-初項}{公比-1}$ 」

これが一番べんり。

たとえば、さっきの $\left( \sum ^{2n}_{k=12}3^{k}\right)$ も、
「 $\dfrac {3^{2n+1}-3^{12}}{3-1}$ 」と瞬殺です。

証明もカンタン。

$x=\left( \sum ^{2n}_{k=12}3^{k}\right)$
とおけば、
$x=3^{12}+3^{13}+3^{14}+\ldots +3^{2n-1}+3^{2n}$ ・・・①
$3x=3^{13}+3^{14}+\ldots +3^{2n}+3^{2n+1}$ ・・・②

② $-$ ①より、
$\left( 3-1\right) x=3^{2n+1}-3^{12}$
$\therefore x=\dfrac {3^{2n+1}-3^{12}}{3-1}$

という感じ。式に公比分だけかけてあげて、元のやつから引けばいいんだね。

さっきのべんりな公式「 $\dfrac {最後の次の項-初項}{公比-1}$ 」を使えば、こんなのも一瞬

$\left( \sum ^{n-1}_{k=2}5\cdot4^{k}\right) =\dfrac {5\cdot 4^{n}-5\cdot 4^{2}}{4-1}$

やっぱり公式は、どうせ覚えるなら日本語でおぼえたほうが汎用性あっていいね。

ちなみに $\sum ^{n}_{k=1}\dfrac {1}{2^{k}}=1-\dfrac {1}{2^{n}}$ だということもわかるけど、
$n$ が無限大に大きくなったらどうなるだろうか。

おそらく $1-0=0$ で $1$ に近づくだろうね！

これって感覚でわかるかな？？小学生にも説明できるように。（小学生は無限に出し続けたらぜったいに大きさも無限大になると信じてる）

一辺のながさが $1$ の正方形を、どんどん半分に折っていくことを考えたら簡単にわかるよ。

こんな感じ。この図から、 $\sum ^{n}_{k=1}\dfrac {1}{2^{k}}=1-\dfrac {1}{2^{n}}$ も計算せずにわかるね。

2016-09-14

覚えなくていい「等差数列の和」

突然だけど、

$\left( \sum ^{n}_{k=1}k\right) =\dfrac {n\left( n+1\right) }{2}$

みたいに習いませんでした？？

じゃあもし、
$\left( \sum ^{n}_{k=11}k\right)$ を計算してくださいと言われたらどうしようか？

少し賢いひとなら、
$\left( \sum ^{n}_{k=1}k\right)-\left( \sum ^{10}_{k=1}k\right)=\dfrac {n\left( n+1\right) }{2}-\dfrac {10\cdot11 }{2}$

ってやるだろうね。

でもどうだろう？？そもそも $\left( \sum ^{n}_{k=11}k\right)$ って
$11+12+\ldots +n$ っていうただの $n-10$ 個の連続した数の和だよね？？

じゃあいきなり
$\dfrac {\left( n+11\right) \left( n-10\right) }{2}$
って計算すればいんじゃないの？？

そう、等差数列の和は
$\dfrac {\left( 初項+最後の項\right) ×個数 }{2}$
で求まる！

理由は簡単。たとえば10から20まで足すこと考えると、
$10+11+12+\ldots +18+19+20$ ・・・①
$20+19+18+\ldots +12+11+10$ ・・・②
こいつらをタテに足してあげれば
$30+30+30+\ldots +30+30+30$
で、 $\left( 10+20\right) ×11=330$ となる。

①と②で同じ式を2個出しちゃったから、最後に $2$ で割ればいい。

というだけ。

さっきも書いた通り、どうせ覚えるんだったら
$\dfrac {\left( 初項+最後の項\right) ×個数 }{2}$
で覚えたほうがいい！

そもそも $\Sigma$ 記号ってなんで使うかっていうと、

・長い数式を短く正確に表現するため
・「\ldots 」とか曖昧な記号を使いたくないから

という理由で、べつに計算しやすくするための記号ではないのだ。

ということで、 $\Sigma$ 記号で書いてあっても基本的には展開した状態で考えた方がわかりやすい。

ちなみに $\Sigma$ の意味だけど

$\left( \sum ^{b}_{k=a}f\left( k\right) \right)$
は、
$k=a,k=a+1,k=a+2,\ldots ,k=b$ を順に $f\left( k\right)$ に代入していって足しあわせる、ということ。

つまり、もしこんな問題が出てきたら

$\left( \sum ^{N}_{k=1}n\right) =?$

$k=1,k=2,k=3,\ldots ,k=N$ を順に $n$ に代入したところで、 $n$ は $n$ のままだから、

$n+n+n+\ldots +n=Nn$

になります。という感じ。ちゃんと記号の意味を考えて、だまされないようにしよう。

2016-09-14

覚えなくていい「解と係数の関係」

二次方程式 $ax^{2}+bx+c=0$ についての解と係数の関係は、ご存知の通り、

$\alpha +\beta =-\dfrac {b}{a}$
$\alpha \beta =\dfrac {c}{a}$

というもの。もちろん $\alpha, \beta$ ってのは二つの解を表してる。

じゃあ三次方程式の解と係数の関係は？と聞かれると、記憶に自信がないか、そもそも知らない人もいるかもしれない。

二次方程式は知ってるのに三次方程式は知らないっていうのはもったないないから、とりあえずまず二次方程式の方はつくれるようにしよう！

ということで証明。

解が $\alpha, \beta$ の二次方程式は

$a\left( x-\alpha \right) \left( x-\beta \right) =0$

とかけるから、これを展開すれば
$ax^{2}-a\left( \alpha +\beta \right) x+a\alpha \beta=0$ となるから、元の方程式とくらべれば

$b=-a\left( \alpha +\beta \right)$
$c=a\alpha \beta$

とわかる。あとは両辺から $a$ を割ってあげれば終了。

めちゃめちゃ簡単だね。ということで次は三次方程式。

三次方程式 $ax^{3}+bx^{2}+cx+d=0$ を考えて、三つの解が $\alpha ,\beta ,\gamma$ だとする。

さっきと同じようにして、
$a\left( x-\alpha \right) \left( x-\beta \right) \left( x-\gamma \right)=0$
$\Leftrightarrow ax^{3}-a\left( \alpha +\beta +\gamma \right) x^{2}+a\left( \alpha \beta +\beta r+\gamma \alpha \right)x$
$-a\alpha\beta\gamma=0$