2016-09-09

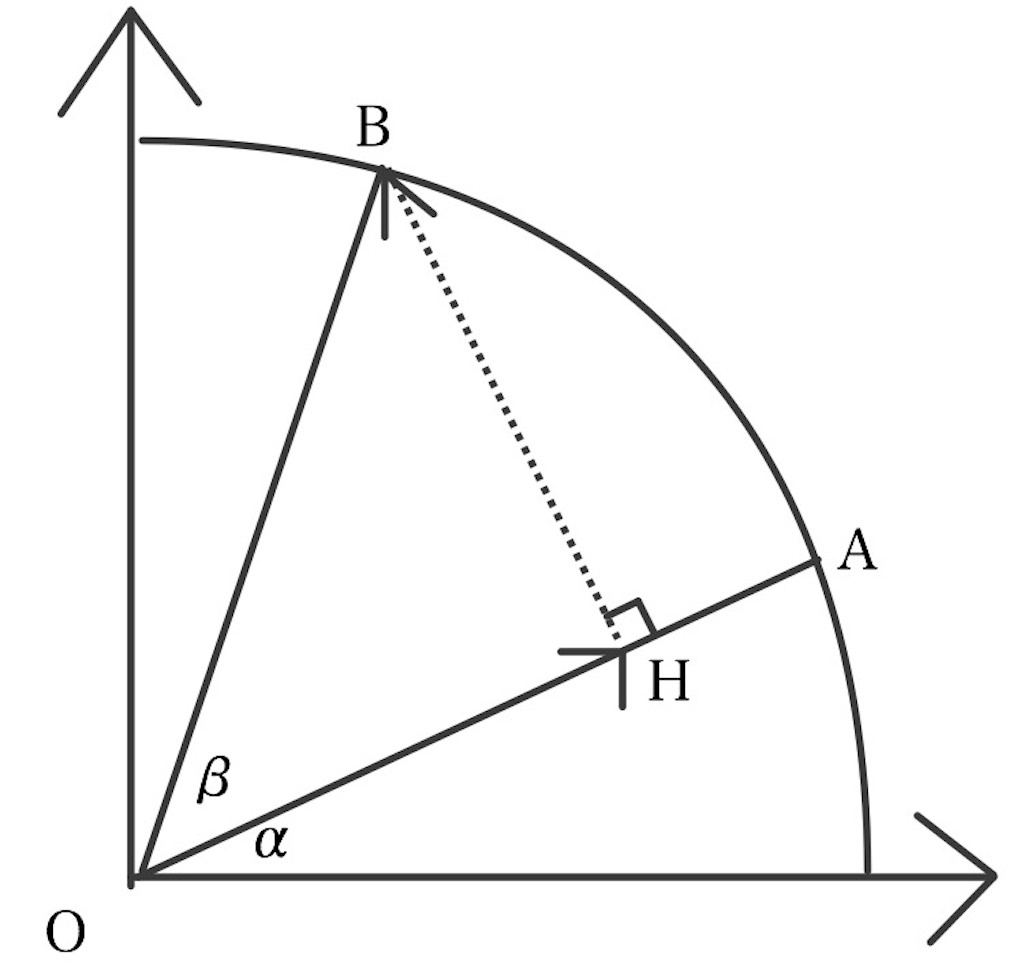
覚えなくていい「三角関数の合成」

覚えなくていい「ベクトル」2（内積） - 算数は得意なのに数学が苦手なひとのためのブログ
の続きですよ！

三角関数の合成って、たぶん高校では $\sin$ で合成するようにならってるはずだけど

世界でみても、割とマイナーらしい。

たしかに教科書に載ってる「使い方」の説明もあんまし腑に落ちないし、、

ということで。

せっかくなら $\cos$ で合成しよう！

やり方は簡単。

$\cos \theta +\sin \theta = \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \cdot \left( \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right) \$

$= \left| \begin{array}{c} 1 \\ 1 \end{array} \right| \cdot \left| \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right| \cos \left( \theta -\dfrac {\pi }{4}\right) \$

$=\sqrt {2}\cos \left( \theta -\dfrac {\pi }{4}\right)$ （下図参照）

簡単ですね。

他に例をあげてみると

$\sqrt {3}\cos \theta +\sin \theta = \left( \begin{array}{c} \sqrt {3} \\ 1 \end{array} \right) \cdot \left( \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right) \$

$= \left| \begin{array}{c} \sqrt {3} \\ 1 \end{array} \right| \cdot \left| \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \right| \cos \left( \theta -\dfrac {\pi }{6}\right) \$

$=2\cos \left( \theta -\dfrac {\pi }{6}\right)$

こんな感じ？わかりますか？

2016-09-08

覚えなくていい「コーシーシュワルツの不等式」

覚えなくていい「ベクトル」2（内積） - 算数は得意なのに数学が苦手なひとのためのブログ
のつづきです。

コーシーシュワルツの不等式ってあまり聞きなれないかもしれないけど、当たり前の式だからなんてことないです。

コーシーシュワルツの不等式は

$ax+by+cy\leq \sqrt {\left( a^{2}+b^{2}+c^{2}\right) \left( x^{2}+y^{2}+z^{2}\right) }$
または
$\left( ax+by+cz\right) ^{2}\leq \left( a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2}\right)$

っていう複雑な式だけど

簡単にいえば

$\overrightarrow {a}\cdot \overrightarrow {x}\leq \left| \overrightarrow {a}\right| \left| \overrightarrow {x}\right|$
$\overrightarrow {a}= \left( \begin{array}{c} a \\ b \\ c \end{array} \right)$ , $\overrightarrow {x}= \left( \begin{array}{c} x \\ y \\ z \end{array} \right)$

というだけ。内積は長さの積以下であるというのは自明です。簡単ですね。

2016-09-08

覚えなくていい「加法定理」

たぶん、学校で加法定理ならったとき多くの先生が「とりあえず覚えろ」っていって

$\cos \left( \alpha +\beta \right) =\cos \alpha \cos \beta -\sin \alpha \sin \beta$
$\sin \left( \alpha +\beta \right) =\sin \alpha \cos \beta +\cos \alpha \sin \beta$

これが当たり前に見えるわけもなく、クラスの怖いI井くんは「ころすころすしねしね..」ってぶつぶついいながら語呂合わせでおぼえてたくらい

ただこれも、「ベクトル＝道順」って知っていればそんな難しいもんじゃない

この四分円を、半径 $1$ の円だと思えば、

$\overrightarrow {OA}= \left( \begin{array}{c} \cos \alpha \\ \sin \alpha \end{array} \right)$
$\overrightarrow {OB}= \left( \begin{array}{c} \cos \left( \alpha +\beta \right) \\ \sin \left( \alpha +\beta \right) \end{array} \right)$

だから、

$\overrightarrow {OB}=\overrightarrow {OH}+\overrightarrow {HB}$

より、 $\overrightarrow {OH}$ と $\overrightarrow {HB}$ が分かれば、なんか加法定理がつくれそうな気がする。

$\overrightarrow {OH}$ は、
方向ベクトルが $\left( \begin{array}{c} \cos \alpha \\ \sin \alpha \end{array} \right)$ で、長さが $\cos \beta$

だから、

$\overrightarrow {OH}=cos \beta \left( \begin{array}{c} \cos \alpha \\ \sin \alpha \end{array} \right)$

$\overrightarrow {HB}$ は、
方向ベクトルが、 $\overrightarrow {OA}$ の左回り $90^{o}$ 回転だから $\left( \begin{array}{c} -sin \alpha \\ \cos \alpha \end{array} \right)$ で、長さが $\sin \beta$

だから、

$\overrightarrow {HB}=\sin \beta \left( \begin{array}{c} -sin \alpha \\ \cos \alpha \end{array} \right)$

以上から、

$\left( \begin{array}{c} \cos \left( \alpha +\beta \right) \\ \sin \left( \alpha +\beta \right) \end{array} \right)=cos \beta \left( \begin{array}{c} \cos \alpha \\ \sin \alpha \end{array} \right)+\sin \beta \left( \begin{array}{c} -sin \alpha \\ \cos \alpha \end{array} \right)$

だから覚えるにしても、この形で覚えたほうが意味もわかってよさそうじゃない？

2016-09-08

覚えなくていい「余弦定理」

余弦定理や、その証明を覚えさせられたかもしれません。

余弦定理はそもそも

$c^{2}=a^{2}+b^{2}-2ab\cos \theta$

というもの。長いし、おぼえたくない！！

ただこれも、ベクトルが道順だってこと知ってれば大したことない。
覚えなくていい「ベクトル」 - 算数は得意なのに数学が苦手なひとのためのブログ

A町からB町いくためには、C町経由していってもいいから、

$\overrightarrow {AB}=\overrightarrow {AC}+\overrightarrow {CB}$

両辺を二乗すれば、（左辺同士、右辺同士で内積をとる）

$\left| \overrightarrow {AB}\right| ^{2}=\left| \overrightarrow {AC}+\overrightarrow {CB}\right| ^{2}$
$=\left| \overrightarrow {AC}\right| ^{2}+\left| \overrightarrow {CB}\right| ^{2}+2\overrightarrow {AC}\cdot \overrightarrow {CB}$
$=\left| \overrightarrow {AC}\right| ^{2}+\left| \overrightarrow {BC}\right| ^{2}-2\overrightarrow {AC}\cdot \overrightarrow {BC}$

よって、
$c^{2}=a^{2}+b^{2}-2ab\cos \theta$
がいえる。

これだけ。長さが知りたかったら、長さと角度が分かってる別のルートを考えて、ベクトルの式を二乗するだけ。

無理して覚える必要ないね

2016-09-08

覚えなくていい「ベクトル」2（内積）

覚えなくていい「ベクトル」 - 算数は得意なのに数学が苦手なひとのためのブログ
前回からの続きです。

ベクトルの内積って習いました？あんまし印象のこってない？

じゃあ、

$\left( \begin{array}{c} a \\ b \end{array} \right) \cdot \left( \begin{array}{c} c \\ d \end{array} \right) = ac+bd \$

はわかるかな？？

分かるっていうのは、知ってるし、しかも当たり前だって思えていること。

っていうとハードル高いか。

そもそも内積ってただのかけ算だからね。

正確にいうと、「同じ方向で考えたときの長さのかけ算」

「長さ×長さ× $\cos \theta$ 」

なんて覚えてるとあんまし役に立たないかも。間違いじゃないけど。

たとえばコレ。

$\overrightarrow {OA} \cdot \overrightarrow {OB}$ はなんですかー？って聞かれたら

即答で

$8×5=40$

要するに、内積をしたかったら、

どちらかのベクトルを基準にして、その方向に進んでいる長さ達を掛けてあげる

今回の場合は $\overrightarrow {OA}$ を基準にしてあげて、 $\overrightarrow {OB}$ は $\overrightarrow {OA}$ （長さ8）方向に5だけ進んでるから、

$8×5$ で瞬殺。

わかりにくかったら、「貢献度」で考えてみよう。

結局内積によって何がわかるかっていうと、基準（ここでは $\overrightarrow {OA}$ ）に対しての貢献度なんだね。

たとえば文化祭で、クラスで出し物をするとしよう。たとえば出し物が多数決でお化け屋敷をすることに決まったとする。

じゃあみんなでお化け屋敷がんばろう！ってなってるときに

・お化け屋敷なんてくだらないものやりたくない！っていってなにもしてないやつは、貢献度 $0$ 。
これは当たり前で、何もしてないから。

・お化け屋敷もいいけど僕は焼きそばを焼くぞ〜！って子は、どれだけ頑張っても貢献度 $0$ 。お化け屋敷に関係ないからね。ベクトルだとこれは直角だね

・お化け屋敷なんて断固反対だ！ベニヤ板すべて破壊する！っていう過激派は、貢献どころか企画が進まないようにがんばるから、貢献度は $-$ （マイナス）。

というかんじ。つまり、

基準のベクトルに対して、貢献してる長さを掛けてあげればいいんだね

じゃあ $\left( \begin{array}{c} a \\ b \end{array} \right)$ と $\left( \begin{array}{c} c \\ d \end{array} \right)$ の内積がなんで
$ac×bd$
になるのかって話だけど。

$\left( \begin{array}{c} a \\ b \end{array} \right) = a \left( \begin{array}{c} 1 \\ 0 \end{array} \right)+b \left( \begin{array}{c} 0 \\ 1 \end{array} \right)$

$\left( \begin{array}{c} c \\ d \end{array} \right) = c \left( \begin{array}{c} 1 \\ 0 \end{array} \right)+d \left( \begin{array}{c} 0 \\ 1 \end{array} \right)$

ってわかりやすく分解してみて、内積の分配法則つかってかけ算してみれば一瞬でわかるよ。（いちおう内積の証明）

ベクトルはよくわかんないときは成分を分解してみるのが正解。

いちおうちゃんと書いときますね。

$\overrightarrow {e_{1}}= \left( \begin{array}{c} 1 \\ 0 \end{array} \right)$

$\overrightarrow {e_{2}}= \left( \begin{array}{c} 0 \\ 1 \end{array} \right)$

って置いとくと（ブログで数式かきやすいように置いただけで大した意味はないです）

$\overrightarrow {e_{1}} \cdot \overrightarrow {e_{1}}=1$ （平行だから1×1）
$\overrightarrow {e_{2}} \cdot \overrightarrow {e_{2}}=1$
$\overrightarrow {e_{1}} \cdot \overrightarrow {e_{2}}=0$ （直交だから0）