覚えなくていい「相加相乗平均の不等式」
相加相乗の不等式で教科書に載ってるのってたぶんこんな感じ。
のとき、
が成り立ち、のとき等号が成り立つ。
これを証明するのはたぶんめっちゃ簡単だと思う。両辺二乗して終わりかな?
じゃあこれは当たり前に見えるかな?
のとき、
等号成立はのとき
これを真正面から証明しようと思ったら大変だけど、実はこれ当たり前の不等式にみえる。
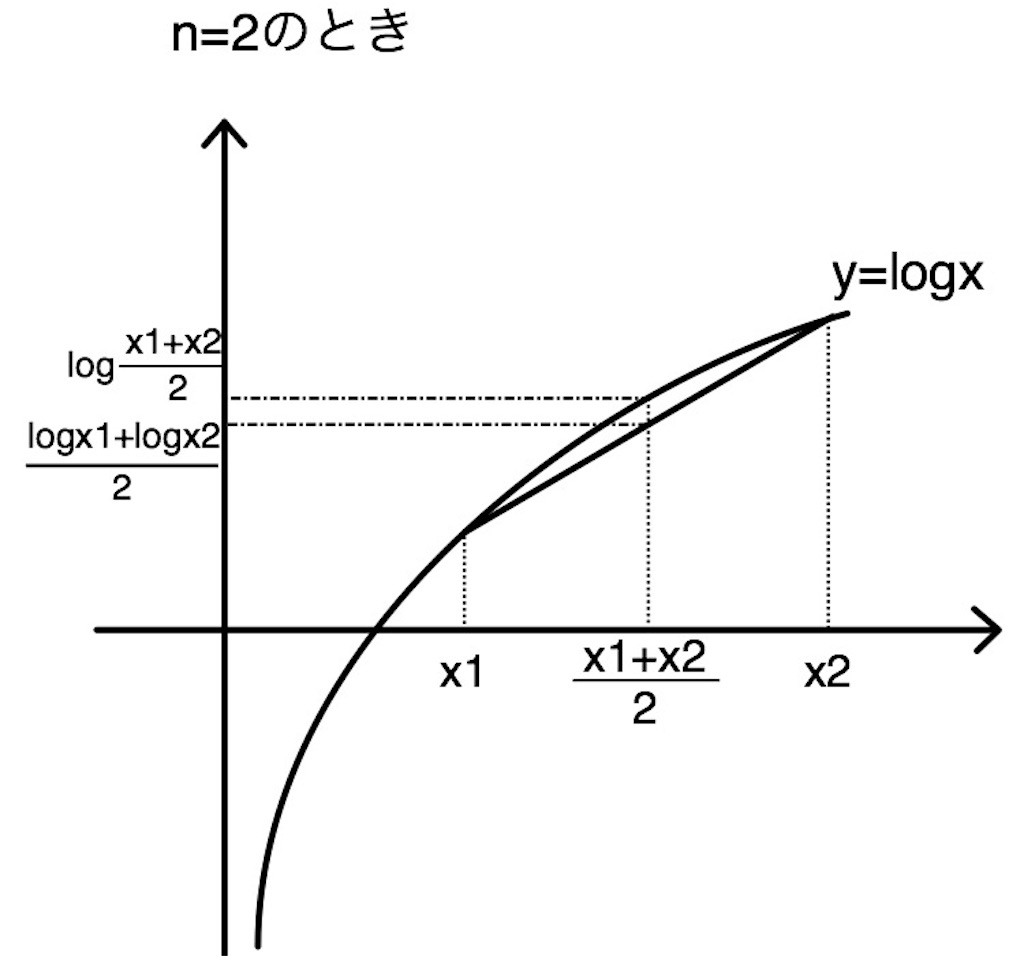
じゃあまずのときを、
のグラフを書いて示してみよう。
グラフより、
となる。のとき等号成立っていうのも図みればわかるね。
じゃあのときはどうだろう?
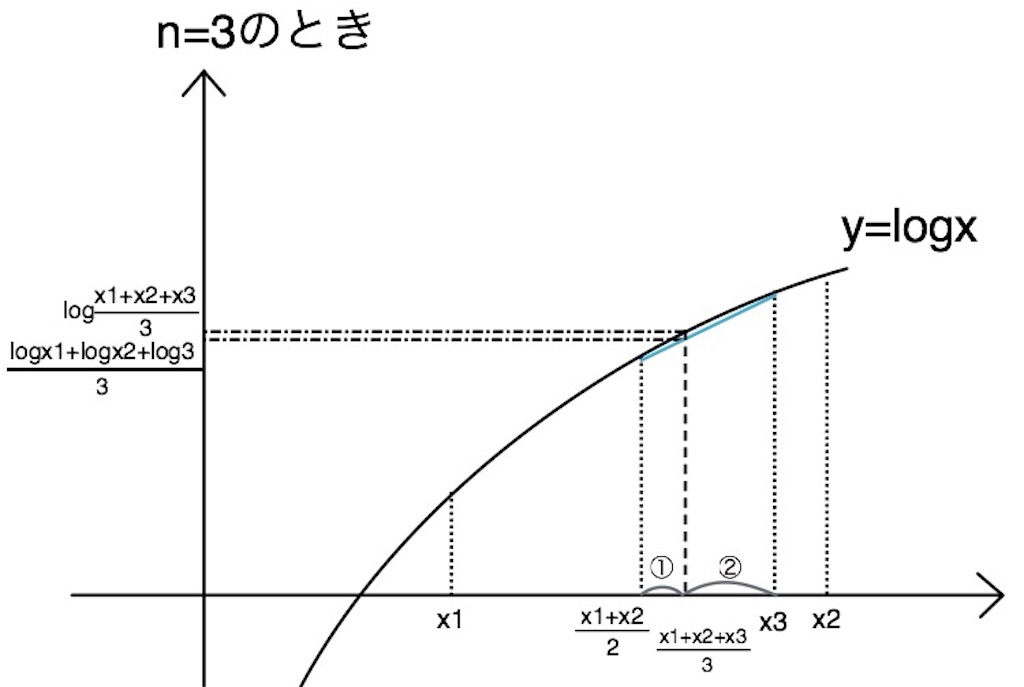
このときも
てなるから確かにこのときも成り立つね。
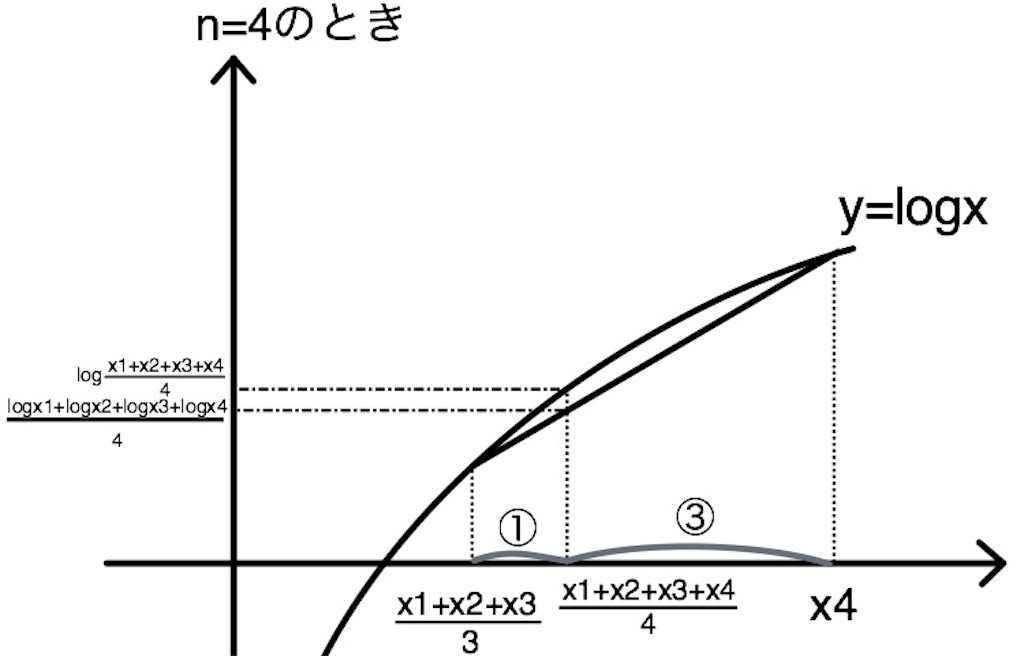
つまりこの作業を繰り返していけば、一般的なについても成り立つね!
ということで、実は相加相乗平均の不等式ってのグラフが常に上に凸であることを利用した不等式なんだ!
よくみると相加相乗の不等式は
でも成り立つのに、わざわざ
て書いてるのは、由来だからなんだね。
相加相乗の不等式は使い方が大事だっていわれるけど、こういうのも知っておいた方が関連した証明問題のときにも役に立つね。